In our previous topics, we have seen
some important concepts such as Concepts of direct and bending stresses, bending
stress in beams, basic concept of shear force and bending moment, strain energy stored in body, beam bending equation, bending stress of composite beam, shear stress distribution diagram for various sections etc.
Now we will be concentrated here a very important
topic i.e. Middle third rule for rectangular section with the help of this
post.
Cement concrete columns are weak under tensile load
and therefore we must be sure that there should not be any tensile load
anywhere in the section and hence load must be applied in such a way that there
will be no tensile stress developed in the section of cement concrete columns.
As we have discussed that when a body
will be subjected with an axial tensile or axial compressive load, there will
be produced only direct stress in the body. Similarly, when a body will be
subjected to a bending moment there will be produced only bending stress in the
body.
Now let us think that a body is
subjected to axial tensile or compressive loads and also to bending moments, in
this situation there will be produced direct stress and bending stress in the
body.
If a column will be subjected with an
eccentric load then there will be developed direct stresses and bending
stresses too in the column and we will determine the resultant stress developed
at any point in the column by adding direct and bending stresses algebraically.
Principle used
We will consider here compressive stress
as positive and tensile stress as negative and we will have the value of resultant
stress at any point in the column section. There will be maximum stress and
minimum stress in the section of column as mentioned here.
σMax = Direct stress + Bending stress
σMax = σd + σb
σMin = Direct stress - Bending stress
σMin = σd - σb
If minimum stress σMin = 0, it indicates that there will be
no stress at the respective point in the section
If minimum stress σMin = Negative, it indicates that there
will be tensile stress at the respective point in the section
If minimum stress σMin = Positive, it indicates that there
will be compressive stress at the respective point in the section
Let us come to the main subject that is Middle third rule for rectangular
section
Let us consider a rectangular section of area A and of
width b and Depth d as displayed in following figure. Let us consider that an eccentric
load P is acting over the rectangular section with eccentricity e with respect
to axis YY.
Minimum stress at any point in the section will be
given by following formula as mentioned here
As we have seen above the various conditions of
minimum stress values and their importance and therefore we can easily say that
minimum stress (σMin) must be greater or equal to zero for no tensile
stress at any point along the width of the column.
Let us analyze the above equation and we will
conclude that in order to not develop any tensile stress at any point in the
section along the width of the column, eccentricity of the load must be less
than or equal to (b/6) with respect to axis YY.
Therefore we can say that if load will be applied
with an eccentricity equal to or less than b/6 from the axis YY and on any side
of the axis YY then there will not be any tensile stress developed in the
column.
Hence range within which load could be applied
without developing any tensile stress at any point of the section along the
width of the column will be b/3 or middle third of the base.
Similarly in order to not develop any tensile stress
at any point in the section along the depth of the column, eccentricity of the
load must be less than or equal to (d/6) with respect to axis XX.
Therefore we can say that if load will be applied
with an eccentricity equal to or less than d/6 from the axis XX and on any side
of the axis XX then there will not be any tensile stress developed in the
column.
Hence range within which load could be applied
without developing any tensile stress at any point of the section along the
depth of the column will be d/3 or middle third of the depth.
Now let us consider that load is eccentric with respect
to axis XX and axis YY both, in this situation load must be applied anywhere
within the rhombus ABCD whose diagonals AC = b/3 and BD= d/3 in order to not develop
any tensile stress at any point in the column.
Area ABCD within which load could be applied without
developing any tensile stress at any point of the section will be termed as Kernel
of the section.
We will discuss Middle quarter rule for circular section in our next post.
Please
comment your feedback and suggestions in comment box provided at the end of
this post.
Reference:
Strength
of material, By R. K. Bansal
Image
Courtesy: Google



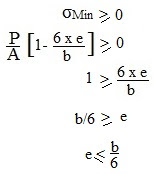












No comments:
Post a Comment